qsort函数的理解与实现(还有冒泡的分析)
本文共 2853 字,大约阅读时间需要 9 分钟。
最近学到qsort,写下来加深自己的理解与记忆。
使用qsort函数,需要库函数<stdlib.h>,通过·qsort可以快速排序,升序或降序看自己的选择。 来个例子,看看怎么回事。 使用qsort#include#include int cmp(const void* e1, const void* e2){ return *(int*)e1 - *(int*)e2;}int main(void){ //struct stu s[3] = { {10,"tom"},{40,"jack"},{20,"tim"} }; int num[9] = { 3,25,6,3,4,7,8,1,2 }; int sz = sizeof(num) / sizeof(num[0]); qsort(num, sz, sizeof(num[0]), cmp); for (int i = 0; i < sz ; i++) printf("%d ",num[i]); return 0;}
qsort( void* arr, size_t num, size_t width, int (*cmp)(const void* element1,const void* element2) )
qsort( 数组首元素,数组元素的个数,每个元素的字节大小,比较函数指针)
就像上面我们要调用cmp这个函数指针,去看是降序还是升序。
cmp要在qsort中调用。如果e1-e2,则是升序,e2-e1,是降序。嘿嘿,至于为什么往下看,我开始也很迷。要了解qsort的运作原理才会明白。void*
介绍一下这个,对初学者应该比较陌生。我们再传递指针时不知道什么类型,用这个可以接收所有类型的指针,到时候要用就强转成想要的类型。像这个
return *(int)e1 - *(int)e2;
实现qsort函数
#include#include void swap(char* a, char* b, int width){ for (int i = 0; i < width; i++) { char tmp = *a; *a = *b; *b = tmp; a++; b++; }}int cmp(void* e1, void* e2){ return *(char*)e2 - *(char*)e1;}void my_sort(void* arr, int sz, int width, int (*cmp)(void* e1,void* e2)){ for (int i = 0; i < sz - 1; i++) { for (int j = 0; j < sz - i - 1; j++) { if(cmp( (char* )arr+j*width,(char* )arr+(j+1)*width)>0) swap((char*)arr + j * width, (char*)arr + (j + 1) * width, width); } }}int main(void){ int arr[] = { 5,3,2,1,5,7,5,3,9,19 }; int sz = sizeof(arr) / sizeof(arr[0]); my_sort(arr, sz, sizeof(arr[0]), cmp); for (int i = 0; i < sz; i++) printf("%d ", arr[i]); return 0;}
再看张图吧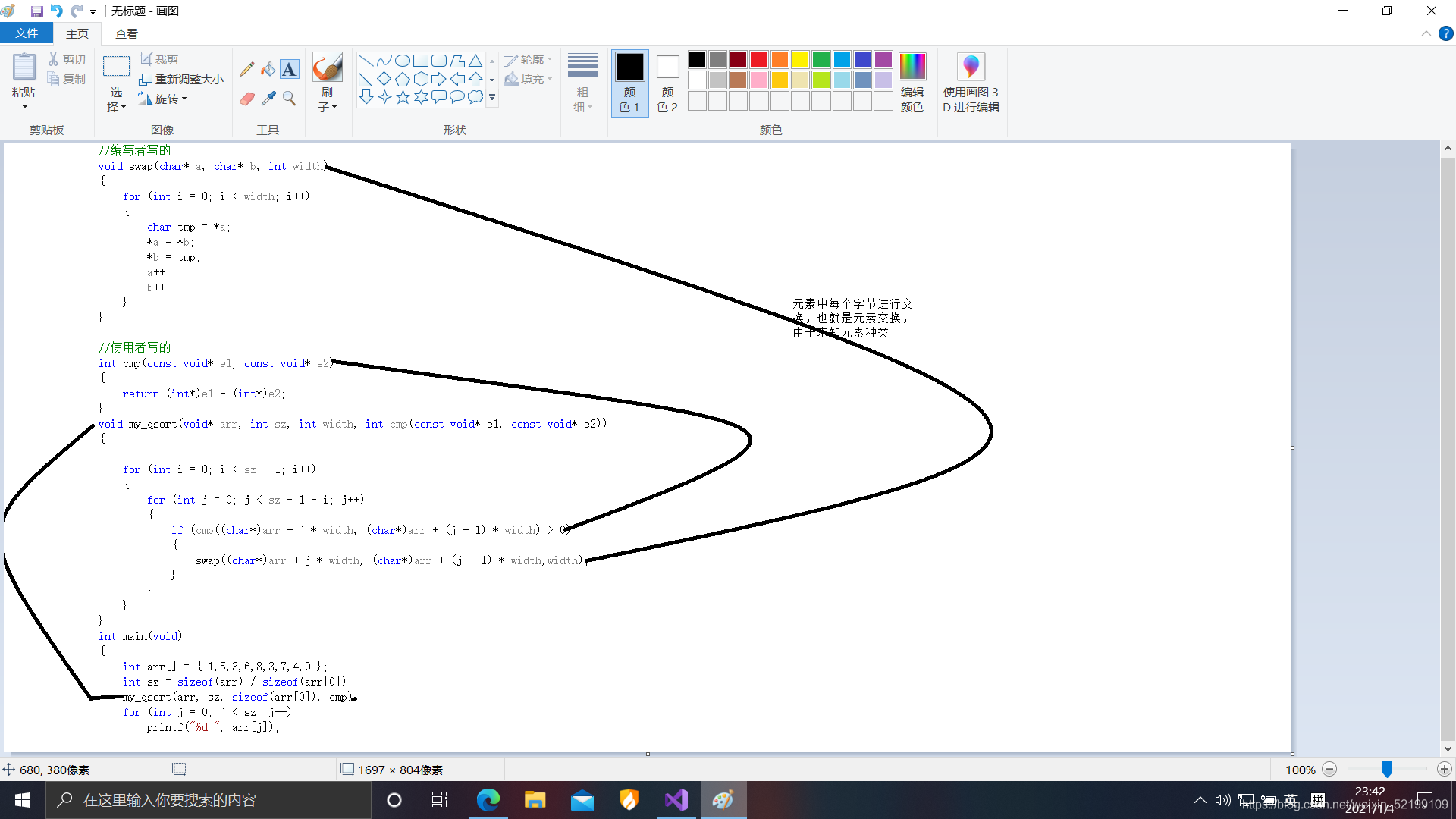
int cmp(void* e1, void* e2){ return *(int*)e1 - *(int*)e2;} my_sort的调用就是qsort。
这串代码是使用者写的,而不是编写者写的,e1,e2强转成什么类型是取决于使用者。再就是my_sort函数的编写。毕竟是循环排序,这就有好多种,冒泡,选择,插入,这个我用冒泡,其实差别不大,主要是为了排序,其实也是可以排字符串的不过往下看,就会知道,只会排首字母。冒泡我再放这分析一下冒泡排序
给一列数 2,3,4,1,9,6,7,8 拿一个天平从数组左边或右边开始比较。根据题目,我们就从左边开始运行。 每比较一次,符合条件就交换(条件取决于你是想要升序还是降序),并且天平向右移动一个范围,就是去与下一个元素比较。,在一路比较下来,拿这种情况来看。升序,最大值一定会移动到最右端。不信,自己试试。如果是降序最小值会移动到最右端。这个别过度研究,有一定认知就行。由此可知,最右端已经拍好。下一轮,依旧是从最左端开始。但是,却可以少比较一个 ——外循环条件是sz-1,代表最多循环sz-1次。 …………比如两个元素排序,只有一趟;三个元素,两趟,不好理解,就这样类比。 ——内循环是负责解决每一次中的比较与交换。同时条件也是sz-1-i,因为每次循环都能排好一个,像这个,第一次排8个元素,比较7次,第二次排7个元素,比较6次 …………因为每次都能将右边排好符合排序要求(升或降)。

if(cmp( (char* )arr+j*width,(char* )arr+(j+1)*width)>0) swap((char*)arr + j * width, (char*)arr + (j + 1) * width, width);
每一次循环,都要比较看是否交换。再进入cmp函数,看上面的步骤图。如果返回值大于零,就进入if中开始交换
如果
e1-e2(前减后)就是升序 e2-e1(后减前)就是降序 这个就不要我解释了吧,好理解。
符合判断条件,就进入swap函数,开始交换。但是编写者并不知道要交换的元素是什么类型,我们只能一个字节一个字节去交换,但我们不知道有多少直接,所以,还传一个元素宽度width。非常贴心。
如果
是字符串。其字符都是一个字节存一个,进行交换。 是数字,也是这么,不过,你可以理解成正常的直接交换,没啥区别。
交换之后还移动到下一个字节,继续交换。
对于结构体啥的,都可以。 好了,应该就这么多了,我要还想到,就再加点。 均使用vs2019进行编译。 如果有问题,烦请大佬指点一二,谢谢。 感谢观看。转载地址:http://brvv.baihongyu.com/
你可能感兴趣的文章
mysql丢失更新问题
查看>>
MySQL两千万数据优化&迁移
查看>>
MySql中 delimiter 详解
查看>>
MYSQL中 find_in_set() 函数用法详解
查看>>
MySQL中auto_increment有什么作用?(IT枫斗者)
查看>>
MySQL中B+Tree索引原理
查看>>
mysql中cast() 和convert()的用法讲解
查看>>
mysql中datetime与timestamp类型有什么区别
查看>>
MySQL中DQL语言的执行顺序
查看>>
mysql中floor函数的作用是什么?
查看>>
MySQL中group by 与 order by 一起使用排序问题
查看>>
mysql中having的用法
查看>>
MySQL中interactive_timeout和wait_timeout的区别
查看>>
mysql中int、bigint、smallint 和 tinyint的区别、char和varchar的区别详细介绍
查看>>
mysql中json_extract的使用方法
查看>>
mysql中json_extract的使用方法
查看>>
mysql中kill掉所有锁表的进程
查看>>
mysql中like % %模糊查询
查看>>
MySql中mvcc学习记录
查看>>
mysql中null和空字符串的区别与问题!
查看>>